速算で大活躍する「補数」とは？

　買い物をする際に、千円札や1万円札で支払ってお釣りをもらうことはよくある。その際、一の位から十の位、百の位へと計算していったら大変だ。

　計算をテキパキとすばやく処理できる人、つまり、速算できる人は、暗算をする際に左から右、つまり上の位から計算をしていく。

　こうした速算の際には、補数が大活躍するので覚えておきたい。

　数学における補数の厳密な定義はややこしいので、ここでは補数を次の意味で使うことにする。

「aのcに対する補数bとは、a＋b＝cを満たすb」

　そして、このcを基準数と呼ぶ。速算では基準数は10､100､1000などのキリのいい数を採用することが多い。

　ちょっと回りくどい言い方だが、具体例でいうと次のようになる。

（1）「9」の10に対する補数は、9＋1＝10より「1」
（2）「2」の100に対する補数は、2＋98＝100より「98」
（3）「995」の1000に対する補数は、995＋5＝1000より「5」

　この例でわかるように、aとbは基準数cに対して互いに補数なのである。
　（1）では「10に対する9の補数は1」、また「10に対する1の補数は9」ともいえる。

　ここで注意したいことがある。それは、基準数より大きな数についても補数を考えるということである。

「aのcに対する補数bとは、a＋b＝cを満たすb」

のことだから、たとえば、「11」の10に対する補数は11＋（－1）＝10より、「－1」ということになる。

　「補数がマイナスの数になる」というのは、ちょっと違和感があるかもしれないが、慣れればなんでもない。元の数がキリのいい数(「キリ数」と名付けます)より大きいために、マイナスする必要が出てきたのだ。ほかにも例を挙げておこう。

（4）「12」の10に対する補数は、12＋（－2）＝10より「－2」
（5）105の100に対する補数は、105＋（－5）＝100より「－5」
（6）1013 の1000 に対する補数は、1013＋（－13）＝1000より「－13」

　なお、キリのよい10、100、1000、10000、...以外にも、場合によっては別の数を「キリ数」として利用することもある。

例）「48」の50に対する補数は、48＋2＝50より「2」

補数を使って釣り銭を計算する

　さて、冒頭で述べた買い物のときのお釣りだが、たとえば1000円の釣り銭であれば、1000に対する補数を求めればよいことになる。

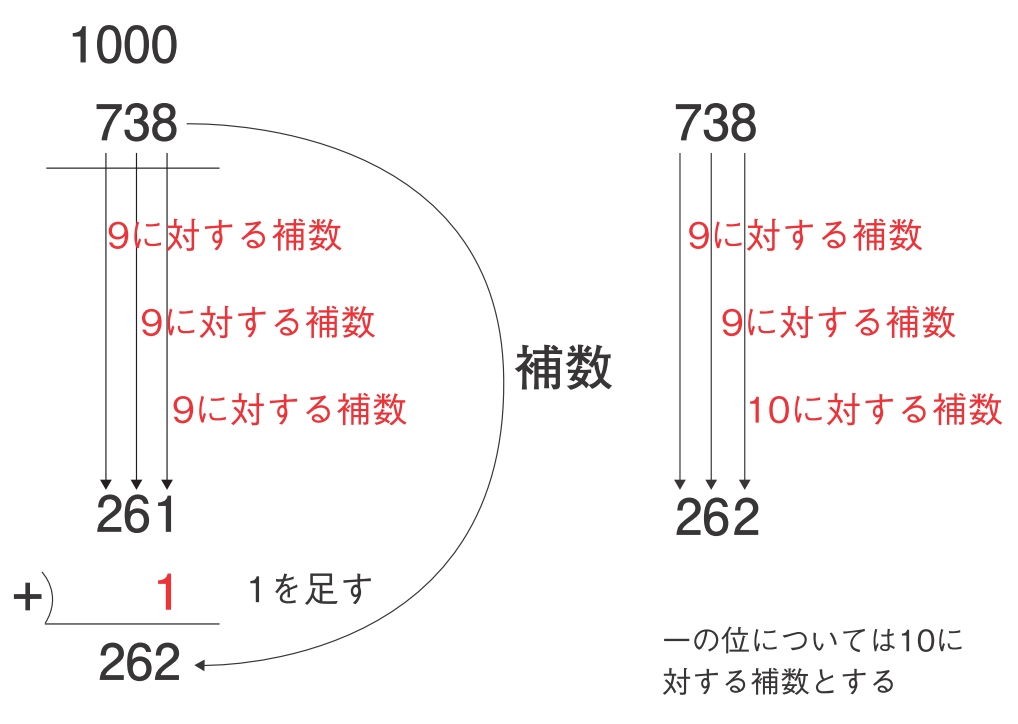
　補数を求め方は簡単だ。たとえば1000に対する738の補数を求めるには、図のように、

「各位の9に対する補数（9との差）を列挙してできた数に1を足す」

だけでよい。言い方を変えれば、

「各位の9に対する補数を列挙する。ただし、一の位については10に対する補数とする」

としてもよい。

　そして、暗算をする際には、上位の位から補数を求めていく。

百の位→7に対する9の補数は「2」
十の位→3に対する9の補数は「6」
一の位→8に対する10の補数は「2」

よって、お釣りは「262」円といった具合だ。

（了）