あなたは3秒で解けますか？

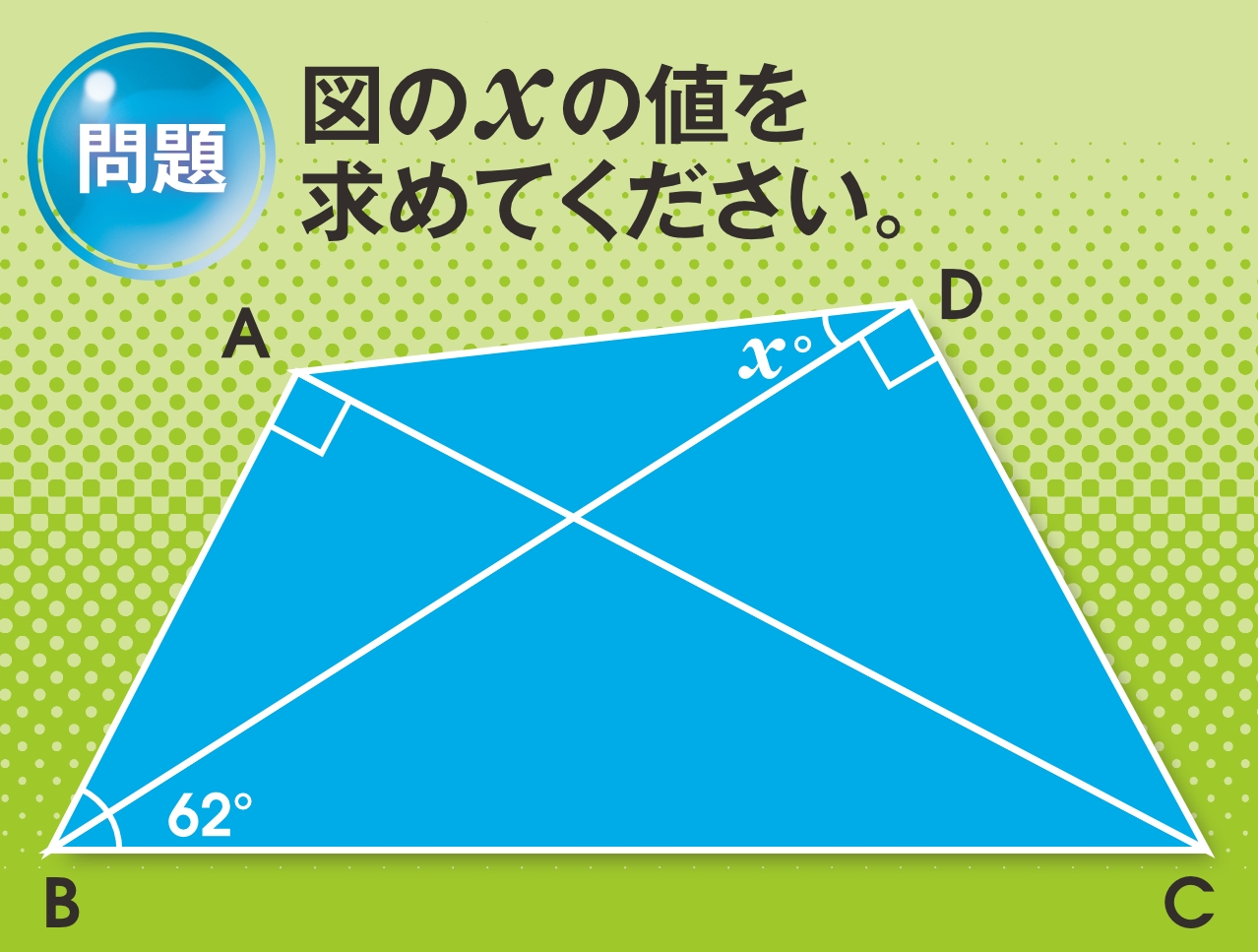
　突然ですが図1を見てください。
　この問題、解けますか？
　数学のできる中学生なら3秒で解くことができる問題です。

　ヒントは、2つの直角三角形に注目してください。

　いかがでしょうか？
　では、もうひとつヒントです。

　直角であることが重要ではなく、この2つが同じ角度になっていることが重要になります。たとえば、これが直角ではなく80度だとしても、同じように解くことができます。

　そろそろ3秒が過ぎたでしょうか。
　答えは、

　180－90－62＝28

で28度になります。

　なぜ、こんな簡単な式で答えが出てくるのでしょうか？
　数学のできる中学生は、次のように考えます。

１）三角形ABCとDCBに注目すると、2つの三角形はBCを共通辺とした直角三角形なので、四角形ABCDは「内接する四角形の条件」を満たしている。
２）内接している四角形の対角の和は180度になるので（内接する四角形の定理）、xは180－90－62＝28度となる。

　また、「内接する四角形の定理」がわからなくても、

１）三角形ABCとDCBに注目すると、2つの三角形はBCを共通辺とした直角三角形なので、2つの三角形は「円周角の定理」から、同じ円に内接していることがわかる。
２）ABCの頂点CとABDの頂点Dも同じ円周上になるので、「円周角の定理」からxと∠ACBは同じ角度になる。
３）三角形の内角の和は180度なので、xは180－90－62＝28度となる。

と答えを導き出すことができます。

　細かな思考方法は人によって多少の違いはありますが、いずれにしても、中学生で習う「円周角の定理」や「内接する四角形の定理」を活用すれば、簡単に解くことができるのです。
　このように中学の数学では、「表面に現れない（背後に潜んでいる）円」を使いこなすことによって、問題に対する美しい解答が得られたり、解答のスピードが格段に違ってきたりします。

「でも、それを知っていてもビジネスで何の役に立つの？」

という方もいるでしょう。

　中学数学を学ぶ目的は、「方程式や関数といった自然科学におけるさまざまな手法」や「論理的な考え方」など、知的な生活を送る基礎を習得することにあります。

　ビジネスなどでも、議論を進める際に重要となる論理的思考や、背後に潜んでいるアイデアの認識などは、幾何の証明を通して訓練することができます。

　そして議論を進めるには、「少数のごく単純な性質から出発して、順を追いながら数多くのより複雑な性質を導いていく」という『ユークリッド原論』をモデルにするのが最適なのです。