「円周角の定理」も小学校で習う算数から導かれる

　詳しい証明方法は割愛しますが、先述の「内接する四角形の定理」である「内接している四角形の対角の和は180度になる」は、「円周角の定理」で簡単に証明することができます。

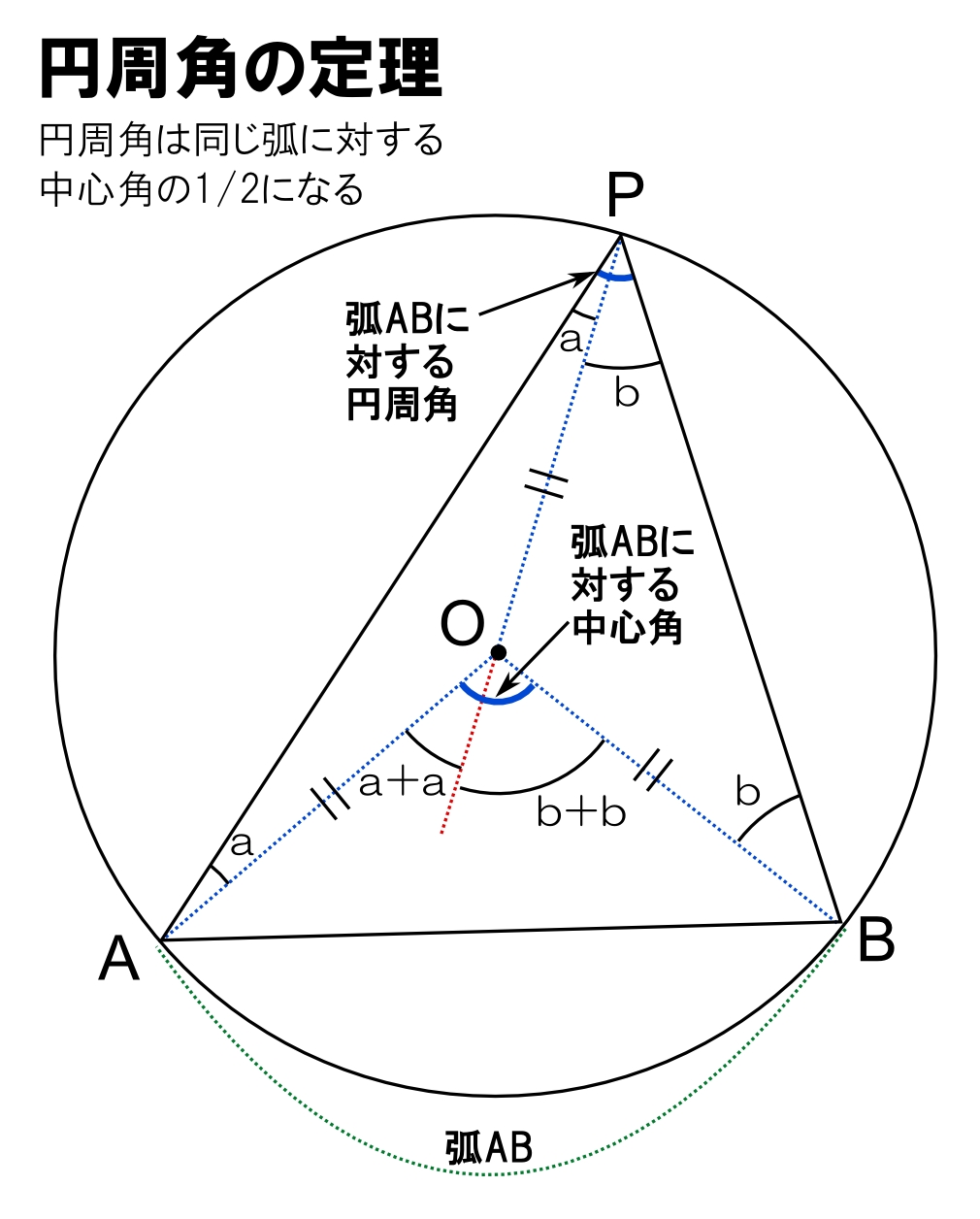
「円周角の定理」とは、「円周角は同じ弧に対する中心角の1/2になる」というものです。

　円の中心をO、円の円周上の点をA、B、Pとしたとき、∠APBを弧ABに対する円周角、∠AOBを弧ABに対する中心角といいます。

　あまりピンと来ない人は、実際に図を書いて考えてみると理解しやすいででしょう。

　まず、円に内接する三角形ABPを作り、円の中心Oから、それぞれの頂点に線を引きます。円の中心Oから引いた線は円の半径になるので、3つの二等辺三角形ができます。

　∠APOをa、∠BPOをbとすると円周角はa＋bになります。

　さらにPOの延長線を書き込むと、「三角形の外角は、その隣にない内角の和に等しい」という三角形の特性から、二等辺三角形APOの頂点Oにおける外角はa＋a、二等辺三角形BPOの頂点Oにおける外角はb＋bとなり、中心角は円周角a＋bの2倍になることがわかります。

　実際に「円周角の定理」を証明するためには、円周角の位置によって3つに場合分けする必要がありますが、なんとなくは証明の方法が理解できたのではないでしょうか。

　また、「三角形の外角は、その隣にない内角の和に等しい」については、「三角形の内角の和は180度になる」という三角形の特性から証明することができます。

　いかがでしょうか。

　このように、難しいと思われた「円周角の定理」も、「三角形の内角の和は180度になる」という小学校で習う単純な三角形の特性から導くことができるのです。

「少数のごく単純な性質から出発して、順を追いながら数多くのより複雑な性質を導いていく」という『ユークリッド原論』における議論の進め方の訓練には、数学の問題や証明が適しているのが、おわかりいただけたのではないでしょうか。

　また数学の問題や証明には、パスルを解くような楽しみがあり、難しい問題を証明したときには体が震えるような感動があります。

　たとえば、中学校で学ぶピタゴラス（三平方）の定理に関連し、350年以上も解けなかったフェルマーの最終定理を、7年間の苦闘の末に解いた数学者の感動の物語は、『フェルマーの最終定理』（サイモン・シン 著）にくわしく書かれています。また、1997年2月8日にNHK教育テレビで放送された『知への旅　解けた！ フェルマーの最終定理』でも紹介されました。

　さあ、あなたも中学数学のやり直しに、チャレンジしてみませんか。

（了）